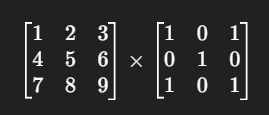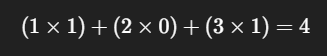From Logic to Linear Algebra: How AI is Rewiring the Computer
For decades, computers were built for logic -- branching decisions, compilers, databases. But AI flipped the script: today's machines are being rebuilt for one thing above all else -- multiplying matrices at massive scale
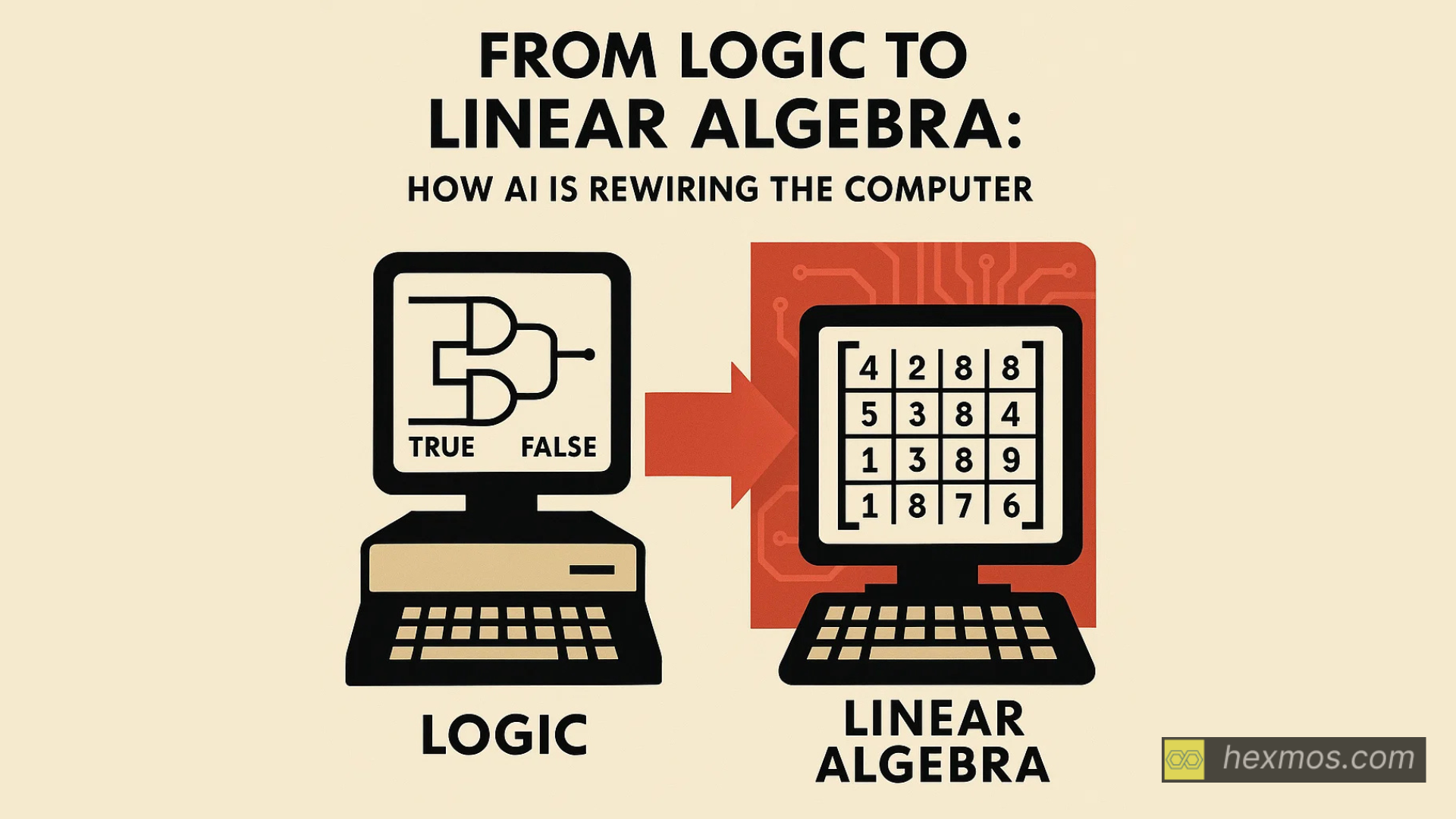
Computers were never just about wires and chips. They've always been built for suiting human imagination - or more practically -- a workload. Or in reverse - the rule is: the workload defines the hardware.
For half a century, workloads looked like this: operating systems making decisions, compilers checking conditions, databases searching records. All of them boiled down to logic -- if this, then that; otherwise, do something else.
The machine for the job was the CPU: fast, flexible, and great at juggling complex, branching tasks.
But AI has upended this. When you open up a modern neural network, you won't see forests of if-else statements. You'll see matrices -- massive grids of numbers. And the work is astonishingly repetitive: multiply, add, multiply, add. Not once, but billions of times.
This quiet shift in workload has triggered a hardware revolution. Computing has begun to move away from chips optimized for logic toward chips optimized for linear algebra.
The Physics Layer: From Sand to Switches
Underneath it all, computing is about materials.
- Copper is a conductor -- it lets electrons flow easily.
- Glass is an insulator -- it blocks electrons entirely.
- Silicon is a semiconductor -- its behavior changes with tiny tweaks ("doping"), letting it sometimes conduct and sometimes insulate.
That trick makes silicon the perfect switch -- the transistor.
The first transistor (Bell Labs, 1947) was thumb-sized. Today, billions can fit on a fingernail. Scaling transistors down has been the foundation of modern computing.
From Transistors to CPUs
One transistor is just a switch. Combine a few, and you get a logic gate (AND, OR, NOT). Chain thousands together, and you can build an arithmetic unit. Stack billions, and you get a processor.
The CPU was designed as a general-purpose workhorse: a Swiss Army knife of computing. It handles operating systems, databases, spreadsheets, video games -- anything you throw at it.
But CPUs are optimized for complex control flow: branches, loops, conditionals. They excel at decision-heavy workloads.
And that's exactly why they stumble on AI.
Why Matrices Took Over
Neural networks are not forests of branches. They're layers of linear algebra.
Take a simple example: multiplying two 3×3 matrices.
To compute just one entry of the result, you multiply a row by a column and add things up:
That's all matrix multiplication is: multiply, then add. Again and again. It's conceptually simple, but the scale is monstrous. A modern AI model requires trillions of these multiplications and additions.
And here's the key shift: AI workloads don't care about clever branching. They care about raw, parallel arithmetic.
This is why CPUs suddenly feel like the wrong tool for the job.
GPUs: Parallelism as a Superpower
The solution came from an unexpected place: graphics cards.
A GPU was originally designed to render pixels in parallel. Where a CPU has a few complex cores, a GPU has thousands of simpler cores, organized for throughput.
Key concepts inside a GPU:
- Streaming Multiprocessor (SM): cluster of cores executing together.
- Warp: group of 32 threads executing in lockstep.
- Memory hierarchy: registers, shared memory, global memory -- structured to keep math units fed.
This makes GPUs perfect for AI. Multiplying matrices looks a lot like drawing pixels: the same operation, repeated millions of times.
- CPU: handle one complex stream of instructions efficiently.
- GPU: handle thousands of simple instruction streams in parallel.
That's why training a neural net might take weeks on CPUs but hours on GPUs.
Beyond GPUs: TPUs and Groq
If GPUs are great, why stop there?
Google's TPU
Google realized GPUs were still too general-purpose. So they built the TPU (Tensor Processing Unit) -- a chip whose circuitry is explicitly designed for tensor math.
- The core is the Matrix Multiply Unit (MXU) -- a systolic array optimized for multiply-accumulate operations.
- Result: higher efficiency, lower cost per AI operation, and reduced power.
Groq
A newer contender, Groq, made a radical design choice: instead of thousands of cores, they built a deterministic dataflow architecture.
- Data streams across the chip like on a conveyor belt, with no scheduling overhead.
- This means predictable latency and high throughput for real-time inference.
Both TPU and Groq show the same theme: hardware bends to the workload.
Understanding FLOPS: A Common Benchmark
Before we compare these machines, we need a common measuring stick. How do you quantify computational power across radically different architectures?
Enter FLOPS -- Floating-Point Operations Per Second.
The Birth of a Benchmark
In the early days of computing, processors handled integers just fine, but real numbers (with decimal points) were a different beast. Scientists needed machines that could handle complex calculations: weather simulations, nuclear physics, engineering designs.
The solution was floating-point arithmetic -- a way to represent real numbers in binary. Think of it as scientific notation for computers:
3.14159becomes something like314159 × 10^-5- The computer stores both the significant digits and the exponent
But floating-point math is computationally expensive. Unlike simple integer addition, floating-point operations require:
- Aligning decimal points
- Performing the operation
- Normalizing the result
- Handling special cases (overflow, underflow, infinity)
Why FLOPS Became the Standard
By the 1960s, scientific computing was dominated by matrix operations -- the same operations driving AI today. Researchers needed a way to compare machines:
- How fast can this computer solve a system of linear equations?
- Which machine can simulate fluid dynamics more efficiently?
- What's the cost-per-calculation for different architectures?
FLOPS provided the answer -- a single number representing how many floating-point calculations a machine could perform each second.
The Scale Problem
Early computers measured in FLOPS (ones). Then came:
- KiloFLOPS (thousands) -- 1970s minicomputers
- MegaFLOPS (millions) -- 1980s workstations
- GigaFLOPS (billions) -- 1990s supercomputers
- TeraFLOPS (trillions) -- 2000s clusters
- PetaFLOPS (quadrillions) -- 2010s supercomputers
- ExaFLOPS (quintillions) -- 2020s frontier machines
Why FLOPS Matter for AI
Modern neural networks are built on floating-point calculations:
- Every neuron activation: floating-point multiply + add
- Every weight update: floating-point arithmetic
- Every matrix multiplication: billions of floating-point operations
When companies train GPTs or users generate huge number of images over time with DALL-E, we're performing petaFLOPS of computation. Hardware that delivers more FLOPS per dollar (and per watt) performs better for these workloads.
FLOPS became a useful benchmark because they measure exactly what AI workloads require: arithmetic throughput.
Comparing the Machines
Let's benchmark the same task: multiplying two large matrices.
| Hardware | Optimized For | Approx Speed | Energy Use | Strength | Weakness |
|---|---|---|---|---|---|
| CPU | Logic-heavy workloads | Few GFLOPs | Moderate | Flexible, runs anything | Poor at AI workloads |
| GPU | Parallel matrix math | 10,000+ GFLOPs | High | Excellent throughput | Expensive, power hungry |
| TPU | Tensor ops (MXUs) | Similar or faster | Medium | Efficiency, tuned for AI | Narrow use case |
| GroqChip | Deterministic dataflow | Competitive (low ms) | Medium-Low | Predictable latency, real-time AI | Ecosystem still maturing |
GFLOPs = billions of floating-point operations per second.
Takeaway: CPUs are versatile, but GPUs, TPUs, and Groq dominate in cost, speed, and energy for matrix math.
Inference Economics
This shift isn't academic -- it's financial.
- CPU inference → slow, costly per operation.
- GPU inference → fast but power-hungry, good for large-scale training.
- TPU inference → highly efficient, cheap at scale (esp. in Google's cloud).
- Groq inference → predictable timing, useful for latency-sensitive tasks like real-time translation.
The hardware you choose doesn't just change performance -- it changes the economics of deploying AI at scale.
Has Computing Changed Forever?
Yes.
For decades, computing meant logic. CPUs reigned supreme.
Now, computing means linear algebra. GPUs, TPUs, and Groq are the new champions.
Does that make CPUs obsolete? Not at all -- they'll always power operating systems, compilers, and general-purpose software. But the center of gravity has shifted.
The deeper lesson: the nature of computing bends to the workload.
Right now, that workload is matrices.